Chaque fois que nous prenons une décision à l’aide de statistiques, il y a quatre résultats possibles, dont deux représentent des décisions correctes et deux des erreurs.
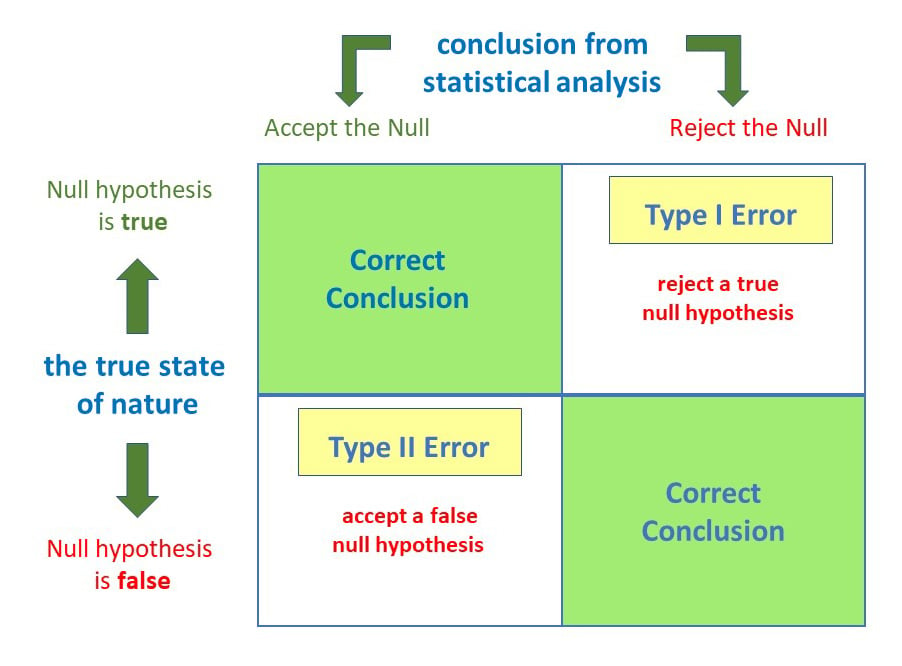
Les risques de commettre ces deux types d’erreurs sont inversement proportionnels : autrement dit, la diminution du taux d’erreurs de type I augmente le taux d’erreurs de type II et vice versa.
Comment se produit une erreur de type 1 ?
Une erreur de type 1 est également connue sous le nom de faux positif et se produit lorsqu’un chercheur rejette à tort une véritable hypothèse nulle.
Cela signifie que vous déclarez que vos résultats sont significatifs alors qu’en fait, ils sont le fruit du hasard.
La probabilité de commettre une erreur de type I est représentée par le niveau alpha (α), qui est la valeur pen dessous de laquelle vous rejetez l’hypothèse nulle.
Une valeur p de 0,05 indique que vous êtes prêt à accepter une probabilité de 5 % de vous tromper lorsque vous rejetez l’hypothèse nulle.
Vous pouvez réduire le risque de commettre une erreur de type I en utilisant une valeur plus faible pour p. Par exemple, une valeur p de 0,01 signifie qu’il y a 1 % de risque de commettre une erreur de type I. Cependant, l’utilisation d’une valeur plus faible pour alpha signifie qu’il y a 1 % de risque de commettre une erreur de type II.
Cependant, l’utilisation d’une valeur plus faible pour alpha signifie que vous aurez moins de chances de détecter une véritable différence si elle existe réellement (risquant ainsi de commettre une erreur de type II).
Comment se produit une erreur de type II ?
Une erreur de type II est également connue sous le nom de faux négatif et se produit lorsqu’un chercheur ne parvient pas à rejeter une hypothèse nulle qui est en réalité fausse.
Dans ce cas, le chercheur conclut qu’il n’y a pas d’effet significatif alors qu’il y en a un.
La probabilité de commettre une erreur de type II est appelée Bêta (β), qui est liée à la puissance du test statistique (puissance = 1- β). Vous pouvez réduire le risque de commettre une erreur de type II en vous assurant que votre test a une puissance suffisante.
Pour ce faire, vous devez vous assurer que la taille de votre échantillon est suffisante pour détecter une différence pratique lorsqu’elle existe réellement.
Pourquoi les erreurs de type I et II sont-elles importantes ?
Les conséquences d’une erreur de type I se traduisent par des changements ou des interventions inutiles qui entraînent une perte de temps, de ressources, etc.
Les erreurs de type II conduisent généralement au maintien du statu quo (c’est-à-dire que les interventions restent les mêmes) alors qu’un changement est nécessaire.



