Le khi-deux (χ2) est utilisé pour tester des hypothèses sur la distribution des observations dans des catégories sans classement inhérent.
Qu’est-ce qu’une statistique du khi-deux ?
Le test du khi-deux (prononcé Kai) examine le schéma des observations et nous indique si certaines combinaisons de catégories sont plus fréquentes que ce que l’on pourrait attendre du hasard, compte tenu du nombre total de fois où chaque catégorie est apparue.
Il recherche une association entre les variables. Nous ne pouvons pas utiliser un coefficient de corrélation pour rechercher des modèles dans ces données, car les catégories ne forment souvent pas un continuum.
Il existe trois principaux types de tests du Khi-deux : les tests d’ajustement, les tests d’indépendance et les tests d’homogénéité. Ces trois tests reposent sur la même formule pour calculer une statistique de test.
Ces tests fonctionnent en déchiffrant les relations entre les ensembles de données observés et les ensembles de données théoriques ou « attendus » qui s’alignent sur l’hypothèse nulle.
Qu’est-ce qu’un tableau de contingence ?
Les tableaux de contingence (également connus sous le nom de tableaux à double entrée) sont des grilles dans lesquelles les données du chi-deux sont organisées et affichées. Ils fournissent une image de base de l’interrelation entre deux variables et peuvent aider à trouver des interactions entre elles.
Dans les tableaux de contingence, une variable et chacune de ses catégories sont listées verticalement, et l’autre variable et chacune de ses catégories sont listées horizontalement.
En outre, l’inclusion des totaux des colonnes et des lignes, également connus sous le nom de « fréquences marginales », facilitera le processus de test du Khi-deux.
Pour que le test du Khi-deux soit considéré comme fiable, chaque cellule de votre tableau de contingence doit avoir une valeur d’au moins cinq.
Chaque test du Khi-deux comportera un tableau de contingence représentant les effectifs observés (voir figure 1) et un tableau de contingence représentant les effectifs attendus (voir figure 2).
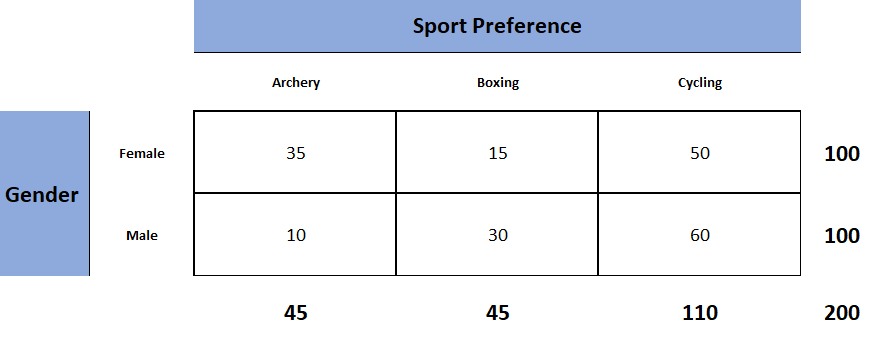
Figure 1. Tableau observé (qui contient les effectifs observés).
Pour obtenir les fréquences attendues pour toute cellule d’un tableau croisé dans lequel les deux variables sont supposées indépendantes, multipliez les totaux des lignes et des colonnes pour cette cellule et divisez le produit par le nombre total de cas dans le tableau.

Figure 2. Tableau attendu (à quoi devrait ressembler le tableau à double entrée si les deux variables catégorielles sont indépendantes).
Pour déterminer si notre valeur calculée pour le χ2 est significative, nous devons également calculer les degrés de liberté de notre tableau de contingence à l’aide de la formule suivante : df= (lignes – 1) x (colonnes – 1).
Calcul de la formule

Calculez la statistique du chi-carré (χ2) en suivant les étapes suivantes :
- Calculez les fréquences attendues et les fréquences observées.
- Pour chaque nombre observé dans le tableau, soustrayez le nombre attendu correspondant (O – E).
- Élever au carré la différence (O – E)².
- Diviser les carrés obtenus pour chaque cellule du tableau par le nombre attendu pour cette cellule (O – E)² / E.
- Additionnez toutes les valeurs de (O – E)² / E. Il s’agit de la statistique du chi-carré.
- Calculez les degrés de liberté du tableau de contingence à l’aide de la formule suivante : df= (lignes – 1) x (colonnes – 1).
Une fois que nous avons calculé les degrés de liberté (df) et la valeur du chi-deux (χ2), nous pouvons utiliser le tableau du χ2 (souvent à la fin d’un livre de statistiques) pour vérifier si notre valeur de χ2 est supérieure à la valeur critique indiquée dans le tableau. Si c’est le cas, notre résultat est significatif au niveau indiqué.
Interprétation des résultats
La statistique du chi-deux vous indique la différence entre le nombre observé dans chaque cellule du tableau et les nombres auxquels vous vous attendriez s’il n’y avait aucune relation dans la population.
Petite statistique du chi-deux : si la statistique du chi-deux est petite et que la valeur p est grande (généralement supérieure à 0,05), cela indique souvent que les fréquences observées dans l’échantillon sont proches de ce que l’on attendrait en vertu de l’hypothèse nulle.
L’hypothèse nulle indique généralement qu’il n’y a pas d’association entre les variables étudiées ou que la distribution observée correspond à la distribution attendue.
En théorie, si les valeurs observées et attendues étaient égales (aucune différence), la statistique du chi carré serait égale à zéro, mais il est peu probable que cela se produise dans la réalité.
Statistique du chi-deux élevée: si la statistique du chi-deux est élevée et que la valeur p est faible (généralement inférieure à 0,05), la conclusion est souvent que les données ne correspondent pas bien au modèle, c’est-à-dire que les valeurs observées et attendues sont significativement différentes. Cela conduit souvent au rejet de l’hypothèse nulle.
Comment rapporter
Pour présenter un résultat de chi-carré dans une section de résultats de style APA, utilisez toujours le modèle suivant :
χ2 ( degrés de liberté, N = taille de l’échantillon ) = valeur de la statistique du khi-deux, p = valeur de p.

Dans le cas de l’exemple ci-dessus, les résultats seraient rédigés comme suit :
Un test d’indépendance du chi-carré a montré qu’il existait une association significative entre le sexe et les projets d’études supérieures, χ2 (4, N = 101) = 54,50, p < 0,001.
Règles de style APA
- N’utilisez pas de zéro avant une décimale lorsque la statistique ne peut être supérieure à 1 (proportion, corrélation, niveau de signification statistique).
- Indiquez les valeurs exactes de p avec deux ou trois décimales (par exemple, p = 0,006, p = 0,03).
- Toutefois, les valeurs p inférieures à 0,001 doivent être indiquées par « p < 0,001"
- Mettez un espace avant et après un opérateur mathématique (par exemple, moins, plus, plus grand que, moins, signe égal).
- Ne pas répéter les statistiques à la fois dans le texte et dans un tableau ou une figure.
interprétation de la valeurp
Vous vérifiez si un χ2 donné est statistiquement significatif en le testant par rapport à une table de distributions du chi-deux, en fonction du nombre de degrés de liberté de votre échantillon, qui est le nombre de catégories moins 1. Le chi-carré suppose que vous disposez d’au moins 5 observations par catégorie.
Si vous utilisez SPSS, vous obtiendrez une valeur p attendue.
Pour un test du chi-carré, une valeur p inférieure ou égale au seuil de signification de 0,05 indique que les valeurs observées sont différentes des valeurs attendues.
Ainsi, des valeurs p faibles (p<0,05) indiquent une différence probable entre la population théorique et l'échantillon collecté. Vous pouvez conclure qu'il existe une relation entre les variables catégorielles. N'oubliez pas que les valeurs p n’indiquent pas la probabilité que l’hypothèse nulle soit vraie, mais plutôt la probabilité d’obtenir la distribution observée de l’échantillon (ou une distribution plus extrême) si l’hypothèse nulle était vraie.
Le niveau de confiance nécessaire pour accepter l’hypothèse nulle ne peut jamais être atteint. Par conséquent, les conclusions doivent choisir de ne pas rejeter l’hypothèse nulle ou d’accepter l’hypothèse alternative, en fonction de la valeur p calculée.
Utilisation de SPSS
Les quatre étapes ci-dessous vous montrent comment analyser vos données à l’aide d’un test d’ adéquation du chi-carré dans SPSS (lorsque vous avez émis l’hypothèse que les proportions attendues sont égales).
Étape 1: Analyze > Nonparametric Tests > Legacy Dialogs > Chi-square… dans le menu supérieur comme indiqué ci-dessous :
Étape 2: Déplacez les catégories de variables dans la boîte « Test Variable List : ».
Étape 3: Si vous souhaitez tester l’hypothèse selon laquelle toutes les catégories ont la même probabilité, cliquez sur « OK »
Étape 4: spécifiez le nombre attendu pour chaque catégorie en cliquant d’abord sur le bouton « Valeurs » sous « Valeurs attendues »
Étape 5: Ensuite, dans la case à droite de « Valeurs », entrez le nombre attendu pour la catégorie 1 et cliquez sur le bouton « Ajouter ». Saisissez ensuite le nombre attendu pour la catégorie 2 et cliquez sur « Ajouter » Continuez ainsi jusqu’à ce que toutes les valeurs attendues aient été saisies.
Étape 6: Cliquez ensuite sur « OK »
Les quatre étapes ci-dessous vous montrent comment analyser vos données à l’aide d’un test d’indépendance du khi-deux dans SPSS Statistics.
Étape 1: Ouvrez la boîte de dialogue Tableaux croisés (Analyze > Descriptive Statistics > Crosstabs).
Étape 2: Sélectionnez les variables que vous souhaitez comparer à l’aide du test du khi-deux. Cliquez sur une variable dans la fenêtre de gauche, puis cliquez sur la flèche en haut pour déplacer la variable. Sélectionnez la variable de ligne et la variable de colonne.
Étape 3: Cliquez sur Statistiques (une nouvelle fenêtre contextuelle apparaît). Cochez Chi-carré, puis cliquez sur Continuer.
Étape 4: (Facultatif) Cochez la case Afficher les diagrammes à barres groupées.
Étape 5: Cliquez sur OK.
Test d’adéquation
Le test d’adéquation du chi carré est utilisé pour comparer un échantillon recueilli au hasard et contenant une seule variable catégorielle à une population plus large.
Ce test est le plus souvent utilisé pour comparer un échantillon aléatoire à la population à partir de laquelle il a été potentiellement collecté.
Le test commence par la création d’une hypothèse nulle et d’une hypothèse alternative. Dans le cas présent, les hypothèses sont les suivantes :
Hypothèse nulle (Ho): L’hypothèse nulle (Ho) est que les fréquences observées sont identiques (à l’exception des variations dues au hasard) aux fréquences attendues. Les données collectées sont conformes à la distribution de la population.
Hypothèse alternative (Ha): Les données collectées ne correspondent pas à la distribution de la population.
L’étape suivante consiste à créer un tableau de contingence qui représente la manière dont les données seraient réparties si l’hypothèse nulle était parfaitement correcte.
L’écart global de l’échantillon par rapport à ces données théoriques/attendues nous permettra de tirer une conclusion, un écart plus important se traduisant par des valeurs p plus faibles.
Test d’indépendance
Le test du Khi-deux pour l’indépendance recherche une association entre deux variables catégorielles au sein d’une même population.
Contrairement au test d’adéquation, le test d’indépendance ne compare pas une seule variable observée à une population théorique, mais plutôt deux variables d’un ensemble d’échantillons l’une par rapport à l’autre.
Les hypothèses d’un test d’indépendance du khi-deux sont les suivantes :
Hypothèse nulle (Ho): Il n’y a pas d’association entre les deux variables catégorielles dans la population concernée.
Hypothèse alternative (Ha): Il n’y a pas d’association entre les deux variables catégorielles dans la population concernée.
L’étape suivante consiste à créer un tableau de contingence des valeurs attendues qui reflète l’apparence d’un ensemble de données correspondant parfaitement à l’hypothèse nulle.
La manière la plus simple de procéder consiste à calculer les fréquences marginales de chaque ligne et de chaque colonne ; la fréquence attendue de chaque cellule est égale à la fréquence marginale de la ligne et de la colonne correspondant à une cellule donnée dans le tableau de contingence observé, divisée par la taille totale de l’échantillon.
Test d’homogénéité
Le test du Khi-deux pour l’homogénéité est organisé et exécuté exactement de la même manière que le test d’indépendance.
La principale différence à retenir entre les deux est que le test d’indépendance recherche une association entre deux variables catégorielles au sein d’une même population, tandis que le test d’homogénéité détermine si la distribution d’une variable est la même dans chacune de plusieurs populations (en attribuant donc la population elle-même comme deuxième variable catégorielle).
Les hypothèses d’un test d’indépendance du khi-deux sont les suivantes :
Hypothèse nulle (Ho): Il n’y a pas de différence dans la distribution d’une variable catégorielle pour plusieurs populations ou traitements.
Hypothèse alternative (Ha): Il existe une différence dans la distribution d’une variable catégorielle pour plusieurs populations ou traitements.
La différence entre ces deux tests peut être un peu difficile à déterminer, en particulier dans les applications pratiques d’un test du Khi-deux. Une règle empirique fiable consiste à déterminer comment les données ont été collectées.
Si les données consistent en un seul échantillon aléatoire dont les observations sont classées selon deux variables catégorielles, il s’agit d’un test d’indépendance. Si les données consistent en plus d’un échantillon aléatoire indépendant, il s’agit d’un test d’homogénéité.



